(c16) 'limit(funmake_no_simp(".",[%pi/2/atan(n),%pi/2/atan(n+1),"","",%pi/2/atan(2*n)]),n,inf)=4^(1/%pi)

(c18) ((3^(3/5)-2^(1/5))^(1/3),%%=subst([5=five,five=5],denest_radicals(%%)))

(c1) (sqrt(2-2^(1/7)),%%=subst([7=seven,seven=7],denest_radicals(%%)))

(c3) (sqrt(127-4*sqrt(6)*7^(1/4)),%%=subst([2=two,two=2],denest_radicals(%%)))

(c27) sum(?mtext(n^-2,cos(9/(%pi*n+sqrt(%pi^2*n^2-9)))),n,1,inf)=-%pi^2/12/%e^3

(c15) (zeta%pi:false,prod(n!/sqrt(2*%pi*(n+1/6))/(n/%e)^n,n,1,inf) =sqrt((1/6)!)*(sqrt(2*%pi*%e)*exp(funmake_no_simp("*",[zeta,?'(2)])/zeta(2)-%gamma))^(1/6))

Illustrating an improvement to Stirling's approximation. The cumulative product of all the error ratios is < 129/128.

(c6) standardize_signs(sin(sum(a[k],k,1,n))=sum(?mtext((-"1")^(k-1)/2/n,prod(2*sin(a[j]-%pi*(k-j)/n),j,1,n)),k,1,n),n)= sum((-1)^k*prod(2*sin(a[j]-%pi*k/(n+1)),j,0,n),k,0,n)/(2*(n+1))

(c247) sum(?mtext((%e)^(%i * %pi * ?mtext(((2 * k + 1)/260)))/(2 * k + 1)^2, product((1 - tan(((%pi * (k + 1/2))/(-2)^n))),n,1,inf)),k,minf,inf) = ((2 * (%pi)^2)/9)

(c104) sum(?mtext((%e)^(%i * %pi * (%edispflag:true,sum(''(funmake_no_simp(".",[''(eipi(k/82))/(2*k+1)^2,prod(1+tan((2*k+1)*%pi/"(- 2)"^n),n,2,inf)])),k,-inf,inf)=funmake_no_simp(".",[%pi^2/eipi(1/164),5/22+%i/62])) 1/2))/(-2)^n))),n,1,inf)),k,minf,inf) = ((2 * (%pi)^2)/9)

(c246) sum(?mtext((%e)^(%i * %pi * ?mtext(((2 * k + 1)/261)))/(2 * k + 1)^2, product((1 - tan(((%pi * ( k + 1/2))/(-2)^(n )))),n,1,inf)),k,minf,inf) = ((2 * (%pi)^2)/9)+?mtext(4474421120+52016651039*%i)/("2"^42 +%i)*(5*%pi^2/36)

(d247) is the special case f = 1/2, d = 1 of

(c229) (radexpand:false,trigsign:false,subst([s=d,m=1/f],sum(((-1)^k*?mtext((%e)^(%i * %pi * ''(?mtext((k + 1/m)/130)))/(( k + 1/m)^2)) * product((1 -s* tan(((%pi * ( k + 1/m))/(-2)^(n )))),n,1,inf)),k,minf,inf) =?mtext((%pi)^2/sin(%pi/m))*?mtext((cot(%pi/m)+(128*s-%i*(s^2-1)*(s^2+1)^3)/(2*(s^2+1)^3+128)))))

(c162) block([radexpand:false],prod((n-2/3)^(1/(n-2/3))/n^(1/n),n,1,inf) =(3^(1/4)*gamma(1/3)^3/4/%e^(%gamma/2)/%pi^2)^(%pi/sqrt(3))/3^(3/4*(2*%gamma+log(3))))

(c175) block([radexpand:false],prod((k-1/6)^(1/(k-1/6))/k^(1/k),k,1,inf) = (4^(7/6)*%pi^2*%e^(%gamma/2)/(3^(1/4)*gamma(1/3)^3))^(sqrt(3)*%pi) /(2^(3*log(3)+log(2)+2*%gamma)*3^(3*(log(3)+2*%gamma)/4)))

(c172) block([radexpand:false],prod((k-5/6)^(1/(k-5/6))/k^(1/k),k,1,inf) = (3^(1/4)*%e^-(%gamma/2)*gamma(1/3)^3/(4^(7/6)*%pi^2))^(sqrt(3)*%pi) /(2^(3*log(3)+log(2)+2*%gamma)*3^(3*(log(3)+2*%gamma)/4)))

(c185) 'integrate(t*log(t^"-2"+1)/(%e^(%pi*t)-1),t,0,inf) =funmake_no_simp("+",[log(%pi)/2,5/6*log(2),funmake_no_simp("*",([-3,zeta,?'(2)]))*%pi^-2,%gamma/2,-5/4])

(c236) standardize_signs(subst(-x,x,sum((-1)^k*x^(3*k)/((3*k+1)!*sin(%pi*k/2+%pi/6)),k,0,inf) = 2*(%e^(sqrt(3)*x/4)+2*sin(x/2-%pi/6)*%e^-(sqrt(3)*x/4))*(2*%e^(sqrt(3)*x/4)*cos(x/2)+%e^-(sqrt(3)*x/4))/(3*sqrt(3)*x)),-sqrt(3)*x/4)

(c237) subst(chebyshev_t=\t, prod(x+b*cos(2*%pi*j/n+g)+a*cos(2*%pi*j/n+f),j,1,n) /(2*a*b*cos(g-f)+b^2+a^2)^(n/2) = chebyshev_t[n](x/sqrt(2*a*b*cos(g-f)+b^2+a^2))/2^(n-1) -chebyshev_t[n](-(b*cos(g)+a*cos(f)) /sqrt(2*a*b*cos(g-f)+b^2+a^2))/2^(n-1))

(c238) subst([chebyshev_t=\t,chebyshev_u=\u],sum(chebyshev_u[n-1](%pi*k*p)/(chebyshev_t[n](%pi*k*p)+cos(a)),k,-inf,inf) =sum(cot(cos((2*%pi*i+a)/n)/p)/n/p,i,0,n-1))

(c239) [\u[n](x) = sin((n+1)*acos(x))/sin(acos(x)), \t[n](x) := cos(n*acos(x))]

(c244) sum(log(k+1/2)^2/(k+1/2)-log(k+1)^2/(k+1),k,0,inf) =funmake_no_simp("+", [-2*log(2)*(3*log(%pi)^2+6*log(2)*log(%pi)+2*log(2)^2)/3, factor(2*%gamma*log(2)^2+2*%gamma^2*log(2)),funmake_no_simp("*",[-4,zeta,"''"(0),log(2)]),-%pi^2*log(2)/6 ])

(c286) (sum(bern(j)/(j*(j+2)!),j,1,inf)=- li[3](1/%e)+zeta(3)-%pi^2/6+3/4,subst([bern(j)=\b[j],li=\li],%%)=dfloat(rhs(%%)))

(c194) ""[4]*\f[3]([a\,,?mtext(a+1/5,?,),?mtext(a+2/5,?,),(5*a/3)+1;"",?mtext(5*a/4+1/2,?,),?mtext(5*a/4+1,?,), 5*a/3],125/128) = csc(%pi/5)*(a/2-3/5)!*(a/2-1/5)!*2^(3*a-2/5)/((a/2-1/2)!*(a/2-3/10)!)

Black belt trig exercise-Solve for F:

(c7) (trigsign:false,subst([a=\a,b=\b,c=\c,d=\d,e=\e,phi=\phi], sin(A-phi)*sin(B-phi)*sin(C-phi)*sin(D-phi)*sin(E-phi)/(sin(A+phi)*sin(B+phi)*sin(C+phi)*sin(D+phi)*sin(E+phi)) =sin(A+B+C+D+E-phi)/sin(A+B+C+D+E+phi)))

Answer:

and

(c9) subst([a=\a,b=\b,c=\c,d=\d,e=\e,phi=\phi],cos(2*phi)=((-sin(2*(e+d+c+b))-sin(2*(e+d+c+a))-sin(2*(e+d+b+a))+sin(2*(e+d))-sin(2*(e+c+b+a))+sin(2*(e+c))+sin(2*(e+b))+sin(2*(e+a))-sin(2*(d+c+b+a))+sin(2*(d+c))+sin(2*(d+b))+sin(2*(d+a))+sin(2*(c+b))+sin(2*(c+a ))+sin(2*(b+a)))/(2*(-sin(2*(e+d+c+b+a))+sin(2*e)+sin(2*d)+sin(2*c)+sin(2*b)+sin(2*a)))))

For a brown belt, just verify the solution. Motivation: this single constraint is sufficient for a generalization of Dougall's theorem:

(c10) sum(''(apply("*",makelist(([a,b,c,d,e,f,a],binom(%%[j]+%%[j+1],%%[j]+k+phi)),j,1,6)))*(k+phi),k,-inf,inf) =gamma(-b-f)*gamma(-c-f)*gamma(-d-f)*sin(2*%pi*phi)*sin(%pi*(f-phi))*sin(%pi*(f+phi))/(a+c)!/(c+e)!/(e+b)!/(b+d)!/(d+a)!/(a+e)!/2/%pi/sin(%pi*(a+f))/sin(%pi*(e+f))

with A=pa,...,E= pe, and F=pf. Ordinary Dougall's also throws in an integer constraint (e.g., f=-a, e=n-a ) so that all but a finite number of terms vanish.

A q-extension of Ramanujan's

where

(c17) (trigsign:false,sum(cot(%pi*j/n+f)*cot(%pi*j/n+g)*cot(%pi*j/n+h),j,1,n)/n[""] = -((sin(2*g-2*f)*cot(h*n)+sin(2*f-2*h)*cot(g*n)+sin(2*h-2*g)*cot(f*n)) /(2*sin(g-f)*sin(f-h)*sin(h-g))+cot(h*n)+cot(g*n)+cot(f*n)))

(c37) funmake_no_simp(nounify('sum),[funmake_no_simp("*",[sqrt(z)-c,funmake_no_simp("^",[sqrt(z),1/2])-c,"...",z^2^(""-n)-c]),n,0,inf]) =(1+z/c)/(1+c)

(c35) prod(4^n^-1*(1/n-1/2)!/sqrt(%pi)/(2/(2*n-1))!,n,1,inf)=4^%gamma

(c39) sum(prod('cot(beta[j]-beta[k]),k,1,n),j,1,n)=sin(n*%pi/2)

(c184) (((x=b/(a-log(x)))=opsubst(\w[1],Lambert_W,part(d183,1,1,2)))=1/(1-sum(b^(""-n-1)*sum((b-a)^k/k!.Stirling_s1[n,n-k+1],k,1,n+1),n,0,inf)))=sum(b^("1"-n)*sum((a-b)^k/k!.sum((-1)^(n-j).Stirling_S1[n,j],j,0,n-k),k,0,n),n,1,inf)

(c215) (intosum(opsubst(\j,bessel_j,(2*sum(bessel_j[2*k](2*k*z)*"'",k,0,inf))=sum(''(diff(bessel_j[2*k](2*k*z),z))/k,k,1,inf)))=taylor(sum(eulerian(2*k+1,k)*(z^(2*k+1)/string(2*k+1)!),k,0,inf),z,0,7))=funmake_no_simp("+",[". . .",funmake_no_simp(".",[binom(7,"3"),z^7/"7"!]),funmake_no_simp(".",[binom(5,"2"),z^5/"5"!]),funmake_no_simp(".",[binom(3,"1"),z^3/"3"!]),funmake_no_simp(".",[binom(1,"0"),z/"1"!])])

(c218) 2*sum((-"")^k.(\j[2*k+1]((2*k+1)*z)/(2*k+1)),k,0,inf)=z*cos(z*cos(z*"..."))

(c313) (powerdisp:true,sum((n*%pi+atan((n*%pi+atan((n*%pi+""^". . .")/3))/3))^"- 2",n,1,inf)=(3*tanh(3*tanh(3*". . .")))^"- 2")=(fpprec:29,apply("",endcons("/ . . .",cons(2,makelist(concat("/",x),x,rest(cf(1/sqrt(1.12252828873058221951129931138826540b-1))))))))*""^"- 2"

Expanding thru a³ gives, e.g.,

(c290) ((cfdisrep(endcons("."["."[" ."]],makelist(c*q^k,k,0,3)))=taylor(((c + 1) * makeprod(sum(((q^((n * (n + 1))/2))/(qpoch( - c, q, q, n))),n,0,inf)/(sum(((q^((n * (n + 1))/2))/(qpoch(q, - c * q, q, n))),n,0,inf)))),q,inf,19))=funmake_no_simp("*",[c+1," "[1],funmake_no_simp(phi[1],[funmake_no_simp("*",[0,"; -",c,";",q]),-q])])/funmake_no_simp("*",[""[1],funmake_no_simp(phi[1],[funmake_no_simp("*",[0,"; -",c,q,";",q]),-q])]))=funmake_no_simp("*",[c+%i," "[1],funmake_no_simp(phi[1],[funmake_no_simp("*",[0,";",%i,c,";","-q"]),q])])/funmake_no_simp("*",[" "[1],funmake_no_simp(phi[1],[funmake_no_simp("*",[0,"; -",%i,c,q,";","-q"]),q])])

(c323) funmake_no_simp("*",[c-1/a," "[1],funmake_no_simp(phi[1],[funmake_no_simp("*",[0,"; ",a,c,";",q]),q])])/funmake_no_simp("*",[""[1],funmake_no_simp(phi[1],[funmake_no_simp("*",[0,"; ",a,c,q,";",q]),q])])=makecf(lambda([n],-1),lambda([n],c*q^n-a-1/a),3)

(c349) sum(tanh(x/2^n)/2^n),n,1,inf) = coth(x) - 1/x

(c418) (sum(atan((-"")^k/k),k,1,inf)=arg(binom(%i,%i/2)) - log(2))= - 0.50667090321662d0

(c422) subst(\e[k],euler(k),euler(k)=sum((-1)^(j-1)*(1-2*j)^k*sum(binom(r,i),i,0,r-j),j,1,r)/2^(r-1))

for r any integer > k.

(c33) (((sum(bernpoly(a+1,k)/(n+a)^(k+1),k,0,inf),((1/n).(1/"1"+(1/(n+1)).(1/"2"+(\2/(n+2)).(1/"3"+(\3/(n+3)).(1/\4+\.\ \.\ \.))))=taylor(%%,n,inf,7))=%%)=funmake_no_simp("+",[sum(bernpoly(a,k)/(n+a)^(k+1),k,0,inf),1/n^2]))=funmake_no_simp("+",[(1/(n+1).(1/"1"+(1/(n+2)).(1/"2"+(\2/(n+3)).(1/\3+\.\ \.\ \.)))),1/n^2]))=psi[1](n)

(c42) sum((k/n).binom(-n,n-k)*fib[k+1],k,">1","")=1

(c45) (%emode:radexpand:false,sum(binom(a,k+phi)*binom(a,k+phi+2*a+1)*exp(%i*(k+phi)*%pi/3),k,-inf,inf)=binom(a,-1/3).(2*cos((a+1/3)*%pi)-exp(%i*(a+2*phi)*%pi))/(3^(3/2)*exp(%i*%pi/6))^(a+1))

(c53) sum(binom(a,3*k+phi)*binom(a,3*k+phi+2*a+1)*(-1)^k,k,-inf,inf)=binom(a,-(a+1)/2)*sin(%pi*(a/2+phi))/3+2*binom(a,-1/3)*(2*sin(%pi*(phi-1/6))*sin(%pi*(5*a/6+2*phi/3))-sin(%pi*(7*a/6+phi/3)))/3^((3*a+5)/2)

(c49) (%emode:false,hyper_f[0,0]([a,-a/2,(1-a)/2,1+a/(%i * sqrt(3) - 2)],[2/3,1-a,a/(%i * sqrt(3) - 2)],4/3/sqrt(3)/eipi(1/6))=eipi(-a/3))

(c67) intosum(sum(prod(1-s*tan((2^m*k+phi)*%pi/"(-2)"^n),n,1,inf)/(2^m*k+phi)^2,k,-inf,inf)/%pi^2)=trigreduce(1/sin(phi*%pi/2^m)^2)*prod((1-s*tan(phi*%pi/"(-2)"^n))/4,n,1,m)

(c81) intosum(sum(prod(1-s*tan((3*k+phi)*%pi/"(-2)"^n),n,1,inf)/(3*k+phi)^2,k,-inf,inf)/%pi^2)=xthru(undistrib(map(trigreduce,multthru(1/(s^2+9)*(cos(phi*%pi)/cos(phi*%pi/3)*s^2+4*sin(phi*%pi/3)*s+3*sin(phi*%pi)/sin(%pi*phi/3))/3/sin(%pi*phi)/sin(%pi*phi/3)))))

(c83) sum((-2)^alpha[2](k)/k^2*prod(1+s*tan(k*%pi/(-2)^(alpha[2](k)+n+1)),n,1,inf),k,-inf,inf)=[%pi^2/6,abs(s)sqrt(3)]

(c87) funmake(":=",[funmake_no_simp("*",[2^alpha[2](k),3^alpha[3](k),5^alpha[5](k),\.\ \.\ \.]),k])

E.g., when s = 0,

(c90) sum((-2)^?2\-powers\-in(k)/k^2,k,1,inf)=%pi^2/12

(c105) prod(2*cos(theta/2^n)-1,n,1,inf)=(1+2*cos(theta))/3

(c106) prod(2*cos(theta/3^n)-1,n,1,inf)=cos(theta/2)

(c107) prod(1+2*sin(theta/"(- 3)"^n),n,1,inf)=cos(theta/2)-sin(theta/2)

(c110) prod((2*cos(theta/3^n)+1)/3,n,1,inf)=funmake_no_simp(".",[2/theta,sin(theta/2)])

(c111) prod((2*cos(theta/3^(n/2))+1)/3,n,1,inf)=funmake_no_simp(".",[1/theta^2/sqrt(3),sin(theta/2)*sin(theta*sqrt(3)/2)])

(c113) prod(2*sin(theta/(- 2)^n+%pi/6),n,1,inf)=funmake_no_simp(".",[2/sqrt(3),cos(theta+%pi/6)])

(c114) prod(1/2+sin(theta/(- 2)^n+%pi/6),n,1,inf)=(2*sin(theta+%pi/6)-1)/sqrt(3)/theta

(c115) prod(4*cos(theta/(-4)^n+%pi/5)*cos(2*theta/(-4)^n+2*%pi/5),n,1,inf)=sin(theta+%pi/5)/sin(%pi/5)

(c172) (powerdisp:true,sum(prod(1+z*sin((k+phi)*%pi/3^n)^2,n,1,inf)/(k+phi).''(eipi(-(k+phi)*9/13)),k,-inf,inf)=(cot(%pi*phi/13)+4*%i/(z^2+4))*%pi)

(c191) sum(((-"")^k/k).prod(cos(%pi*k/(-2)^n)-s*sin(%pi*k/(-2)^n),n,">1",""),k,-inf,inf)=-%pi*s/3

(c199) sum((''(eipi(k/3))/k).prod(cos(%pi*k/(-2)^n)-s*sin(%pi*k/(-2)^n),n,">1",""),k,-inf,inf)=(%pi/3)*expand(-(s+%i)*%i)*s/(%i*s+3)

(c302) (funmake(pderivop(zeta, 3),[1/2]) = ((zeta(1/2)*(224*zeta(3)-(2*log(8*%pi)-%pi+2*%gamma)*(4*(log(8*%pi)+%pi+%gamma)^2+3*%pi^2)))/32)+((3*funmake(pderivop(zeta,2),[1/2])*(2*log(8*%pi)+%pi+2*%gamma))/4),%%=dfloat(eval(rhs(%%))))

(c306) (radexpand:False,sum(''(funmake(pderivop(zeta,1),[1-2*n]))*(-%pi^2)^n/(2*n+1)!,n,1,inf)=(log(%pi)-1)*(log(2*%pi)+%gamma)+factor(1/2+log(2)^2/2+log(2))+funmake(pderivop(zeta,2),[0])+1/2,%%=dfloat(eval(rhs(%%))))

(c350) -theta[2](0,q^(1/2))/funmake(pderivop(theta[2],0,1),[0,q^(1/2)])/q^(1/2)=log(q)+8*%pi^2*%e^(2*%pi^2/log(q))+\.\ \.\ \.

E.g., for q = .5,

(c349) (subst(\.5,q,part(%,2,2)),%%=dfloat(subst(.5,\.5,%%)))

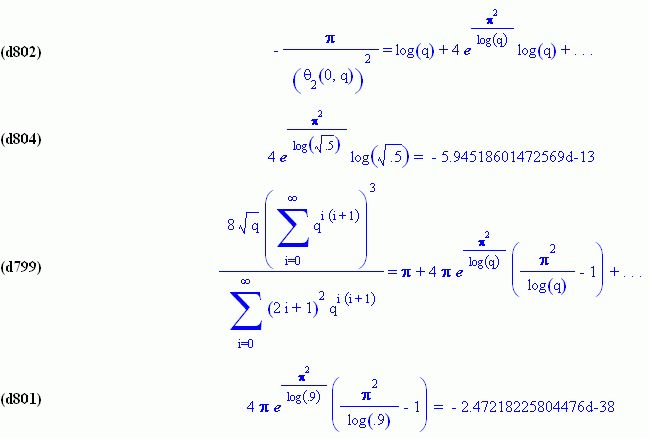
(c796) (powerdisp:false,'integrate(log(subst(\t,chebyshef_t,chebyshef_t)[n](x)-a),x)=sum((x-cos((2*%pi*k+acos(a))/n))*log(x-cos((2*%pi*k+acos(a))/n)),k,0,n-1)+(log(2)*(n-1)-n)*x)

(c1024) subst("1/3",1/3,'integrate(log(u!),u,0,1/3)=log(2*%pi)/6-25*log(3)/72+sqrt(3)*psi[1](1/3)/(36*%pi)-4*zetaderiv(-1)/3-sqrt(3)*%pi/54-2/9)

(c1026) subst([psi[1](1/3)=psi[1]("1/3"),2/3="2/3"],integrate(log(u!),u,0,(2/3))=log(8*%pi)/3-49*log(3)/72-sqrt(3)*psi[1](1/3)/(36*%pi)-4*zetaderiv(-1)/3+sqrt(3)*%pi/54-5/9)

(c1045) subst([%catalan=lambda,1/8="1/8"],'integrate(t*log(sin(%pi*t)),t,0,1/8)=sqrt(2)*(psi[2](1/8)-4*%pi*psi[1](1/8))/2048/%pi^2+(4*sqrt(2)+5)*%pi/512+%catalan*(2*sqrt(2)-1)/64/%pi+7*(16*sqrt(2)+37)*zeta(3)/1024/%pi^2-log(2)/128)

I.e., # unordered partitions of n into 8 triangular numbers = (n+1)³ times the sum of the cubes of the reciprocals of the odd divisors of n+1.

(c1212) sum(cos(%pi*sqrt(n^2+1))/(-1)^n/n^2,n,1,inf)=%pi^2/12

(c1222) stringpoch(sum((1-a*b*c*q^(3*n-1))*qpoch(a*b*c/q,q^2,n)*qpoch(a,b,c,q,n)*q^binom(n+1,2)/qpoch(q,q,n)/qpoch(b*c*q,c*a*q,a*b*q,q^2,n),n,0,inf)=qpoch(a*b*c/q,a*q,b*q,c*q,q^2,inf)/qpoch(q,b*c*q,c*a*q,a*b*q,q^2,inf))